こんちくわ。データ分析部兼サウンドエンジニアの大曽根です。最近は吾妻光良&The Swingin Buppersのライブに行きました。
今回は4/12に開催した「これからの強化学習」の輪読会の1.3節で紹介した価値反復法のアルゴリズムを、教科書とは異なる例で実装してみました。
開催報告については下記のブログをご覧ください。
メジャーなゲームである三目並べを、1.3節にて紹介されているSarsaを用いて学習しました。 教科書とは別の例で実装することで少しでも理解が深まればと思います。
価値反復に基づくアルゴリズム
マルコフ決定過程において価値関数を特定の更新式に従って更新する手法です。(今回はSarsaで試しました。) 発表の際には、tの状態の更新式に次の状態 t+1が含まれているところなどがわかりづらいとの質問を受けました。 価値反復に基づくアルゴリズムでは過去の事例(エピソード)における、次の状態を参考に現在の行動価値関数を変更していくのでその点がわかりづらいかもしれません。
実装
エージェントと対戦相手が特定の座標に交互に手を打っていく形式になります。 (こういう類のシミュレーションでは)先行と後攻を固定する場合もありますが、今回は先行と後攻を対戦ごとに交代する形式の実装にしています。 また、すでに自身もしくは対戦相手が打った場所には手を打たない制御を入れています。
環境
盤面の座標および○×がどこに置かれているか 実際のコードでは ○: 1、×: - 1、空白: 0の3つの値を持つlistで表現しました
s = [ 0, 0, 0, 0, 0, 0, 0, 0, 0]
単純に考えると39通りの状態が考えられ、3目並べ程度のゲームで意外に環境の取りうる範囲は広いことがわかるかと思います。 (実際には存在しない手もあるのでもっと少なくなります。)
行動:
自身の手順の際にs の配列のどこを変更するかを行動としています。 上述の通り環境sの0 (○×のいずれも打たれていない場所) にしか打たない制御をしています。
A = [ 0, 1, 2, 3, 4, 5, 6, 7, 8]
報酬: 勝敗
報酬は勝敗が決定した際のみに振り分けられるものとし、勝利した際(○が3つ並んだ場合)にはプラスの報酬、負けた際(×が3つ並んだ場合)にはマイナスの報酬を振り分けられるようにしました。

また、引き分けの際には報酬なしに設定しました(ここのルール設定によって学習の挙動が異なるかもしれません)。
学習のイメージ

下記の例の場合には正の報酬を得ることができます。
s = [1, 1, 1, 0, -1, 0, 0, -1, 0]
ですので
sn = [ 1, 1, 0, 0, -1, 0, 0, -1, 0]
の際の
an = 2
の場合は勝利することができる(報酬が獲得できる)ため、 Q[sn][an] の価値関数が高くなれば学習が成功していると言えます。
これを繰り返して行くと次の状態価値関数を別のエピソードでフィードバックすることができます。
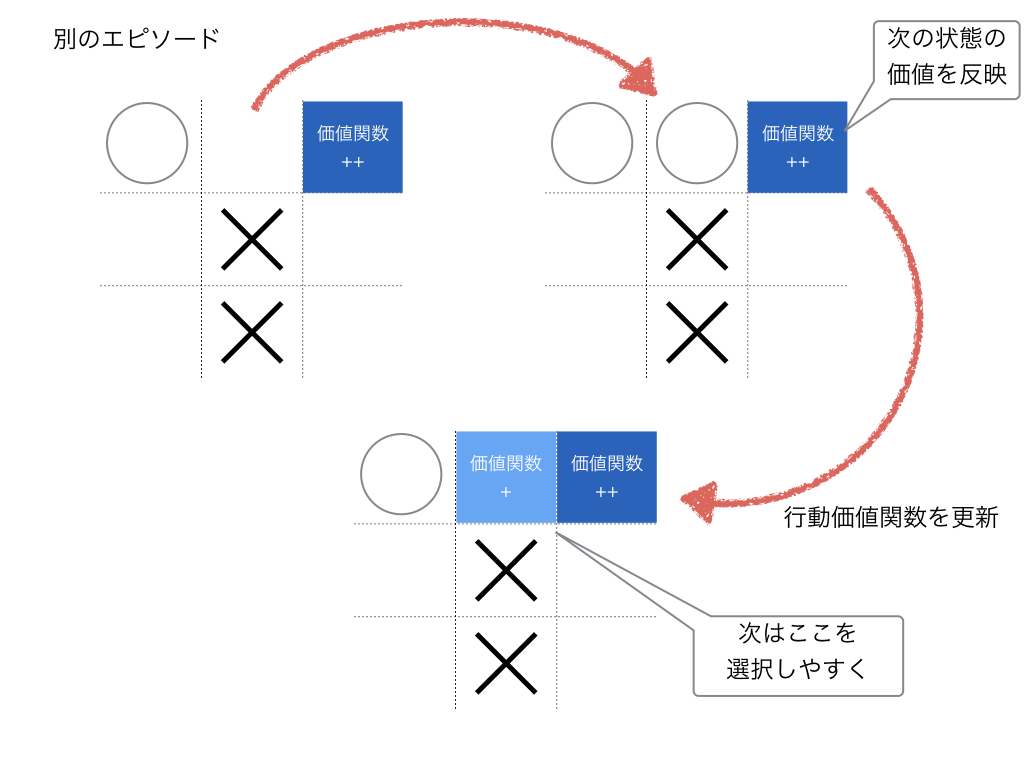
方策
どの手を打つかの戦略を方策としています。Q値が高いものを打つパターンと、一定確率でランダムの戦略を打つ場合(ε-greedy)の二つを用意しました。
結果
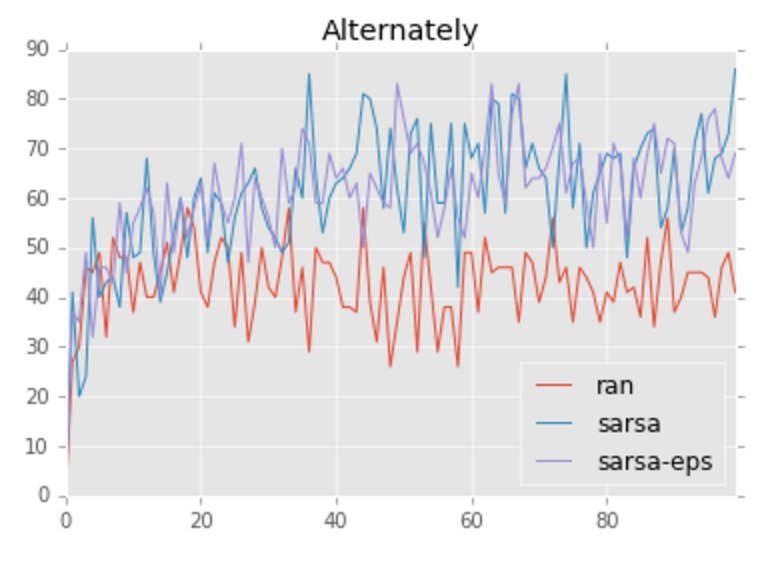
学習に関するパラメータはα = 0.2、γ = 0.8で設定しトータルで10,000ゲームを行い、
- ベースラインとして用意した完全ランダムのアルゴリズム
- sarsa
- sarsa ε-greedy (ε = 10%)
の三種類のアルゴリズムで100試合ごとの勝率をplotしました。 完全ランダムの場合と比較しますると、sarsaのアルゴリズムの場合には徐々に勝率が高くなっていることがわかるかと思います。 今回の例ではあまりgreedyとε-greedyとの間に大きな差はありません。 (plotをみる限りは学習(収束)が割とはやいので探索に対するメリットがないのかもしれません)
考察
初期の盤面のQ値をあまり学習できていなかったので、
- 初期の盤面のみルールを与える
- リーチの時点で少し報酬をあたえるなど
なども試してみると面白いかと思いました。
感想
非常にシンプルなゲームですが、ターンの概念や勝敗判定などゲームの基礎的な部分の実装に以外と時間がかかってしまいました。 強化学習は環境の設定と報酬の設定など、本で読むより実装すると気づく部分も多いかと思います。全てを実装する必要はないかと思いますが、本を読みつつ実装してみるのも学びを進める上では重要かと思います。
今後
他のゲームの実装や、学習過程の可視化なども試して行きたいです。