Gunosyデータ分析ブログ

Gunosyで働くデータエンジニアが知見を共有するブログです。

より正しい意思決定のための統計的仮説検定とサンプルサイズ計算

はじめに

こんにちは、Gunosy Tech LabのBIチームに所属しているクボタです。 Gunosyではアプリ内のロジックやUI等の変更において数値ベースでの意思決定を行なっています。 例えば新たなキャンペーンでのCVR増加やUI変更によるA/Bテストでのクリック数増加の効果検証などで統計的に裏打された手法を用いることで正しく意思決定を行うことを目指しています。

data.gunosy.io

本記事ではそのような状況で必要となるサンプルサイズの設計や統計的仮説検定のお話をさせていただきます。

検定手法の選択

数値による意思決定を行う際に検定はよく利用されており、現在ではデータがあればRやPythonなどを利用して簡単に結果を知ることが出来ます。 しかし、検定の手法には様々な種類がありケースによって適切な手法を選択する必要があります。 手法を選ぶ要素としては主に以下のようなものが考えられます。

  • パラメトリック or ノンパラメトリック

  • 収集可能なサンプルサイズ

  • 比較する統計量の種類

  • 母分散の既知性

  • 比較する群の等分散性

  • 比較する群の数

これらの状況によって適切な検定の手法を選んで意思決定を行う必要があります。

最初に良くあるケースとして分散が未知の独立した2群の母平均の差の検定を以下のような順番で見ていきたいと思います。

統計的仮説検定の手順

  1. 比較する指標の決定
  2. 帰無仮説 H_0と対立仮説 H_1の決定
  3. 検定統計量の決定
  4. 有意水準 \alphaの決定
  5. 効果量の決定
  6. 検出力 1-\betaの決定
  7. サンプルサイズの計算

比較する指標の選定

まず始めに2群を比較する指標を決めます。 指標はCVRや継続率などプロダクトの改良によって変化が期待される数値を選びます。 ここでは2群の平均値 \mu_0, \mu_1 の差の検定に帰着するケースを想定します。

帰無仮説 H_0と対立仮説 H_1の決定

検定では限定的に定義された帰無仮説 H_0と、それが棄却された際に採択される対立仮説 H_1を設定します。 例えばUI変更を行った時に H_0はclickに変化がない場合、 H_1は変化があった場合になります。 現在考えているケースでは、以下のように平均に変化のない H_0と2群で平均が異なる両側 or 片側の H_1を設定します。

  • 帰無仮説 H_0 \mu_0=\mu_1
  • 対立仮説(両側検定) H_1 \mu_0\neq\mu_1
  • 対立仮説(片側検定) H_1 \mu_0\geq\mu_1
  • 対立仮説(片側検定) H_1 \mu_0\leq\mu_1

検定統計量の選定

検定の際に使用する統計量は比較したい指標と検定方法の選択に伴い決まります。 正規分布に従うデータの標本分散 V、サンプルサイズ n、標本平均値 \bar{X}、母平均 \muで構成される t = \frac{\bar{X} - \mu}{\sqrt{V/n}}は自由度n-1のt分布に従います。 この統計量を利用して平均値に関するt検定を行うことが出来ます。 2群が等分散の場合は以下のt値は自由度 n_0 + n_1-2 のt分布に従います。

t=\frac{\bar{X_1}-\bar{X_0}}{\sqrt{V(\frac{1}{n_0}+\frac{1}{n_1})}}

ここで \bar{X_i}は標本平均、 V = \frac{S_0 + S_1}{n_1+n_2-2}、 S_i = \sum_{k=1}^{n_i}(X_{ik} - \bar{X_i})^2 は分散、 n_iはサンプルサイズです。 X_iは必ずしも正規分布とは限りませんが標本平均 \bar{X_i}はサンプルサイズが小さくない場合は、中心極限定理のため正規分布に漸近するため上記の tはt分布として扱えます。データの正規性の確認が必要な場合はシンプルにヒストグラムでの可視化による方法やShapiro-Wilk検定(scipy.stats.shapiro)やKolmogorov–Smirnov検定(scipy.stats.kstest)で行うことができます。(※()内はPythonのライブラリ)

等分散とは言えない場合はそれを考慮に入れた以下のようなウェルチのt検定を使います。

t_0=\frac{\bar{X_1}-\bar{X_0}}{\sqrt{(\frac{V_0}{n_0}+\frac{V_1}{n_1})}}

ここで V_i = \frac{S_i}{n_i-1}、自由度は \phi=(\frac{V_0}{n_0}+\frac{V_1}{n_1})^2/(\frac{V_0^2}{n_0^2(n_0-1)}+\frac{V_1^2}{n_1^2(n_1-1)})となります。 独立な2群のt検定はPythonではscipy.stats.ttest_indで行えます。 ウェルチのt検定はパラメーターのequal_varをFalseに指定することで行えます。 以下はPythonでの例です。

from scipy import stats
stats.ttest_ind(X_0, X_1) t検定(等分散)
stats.ttest_ind(X_0, X_1, equal_var = False)  ウェルチのt検定

2群の等分散性の確認は標準偏差の比がF分布になることを利用したF検定で行えます。しかし、等分散検定とt検定を続けて行うことは後に述べる多重検定と同様に結果を歪める可能性があるためウェルチのt検定を最初から使うのが良いようです。

有意水準 \alphaの決定

有意水準 \alphaは、最終的にp値と比較して \alpha以下ならば H_0を棄却します。 慣例では5%に設定することが多いようですが、様々な議論があり分野や扱う問題によって異なるようです。 \alphaは帰無仮説が正しい場合に誤って棄却してしまう確率(第1種の過誤, false positive rate)であり、帰無仮説が正しい場合でも \alphaの確率で対立仮説を採択してしまうことを意味しています。 \alphaが小さいほど誤って棄却する確率減少しますが、 \betaを対立仮説が正しい場合に帰無仮説を棄却しない確率(第2種の過誤, false negative rate)とした時に、検出力 1-\beta (正しく対立仮説を採択する確率)は低くなります。 よって、有意水準 \alphaと同時に検出力 1-\betaを考慮に入れる必要があります。

f:id:khirohisa:20180418123432p:plain:w400

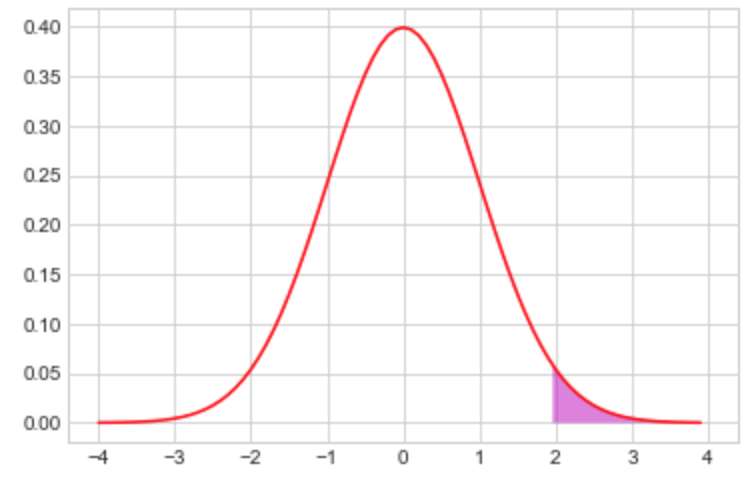
図は帰無仮説における t_0の分布(正規近似)で紫色の領域は片側検定での有意水準5%です。

検出力 1-\betaの決定

実験において第2種の過誤を管理するために有意水準と同様に検出力を事前に固定します。慣例では80%程度にすることが多いようです。

f:id:khirohisa:20180418124204p:plain:w400

図は \mu_0\leq\mu_1の片側検定における帰無仮説(赤)と対立仮説(青)における正規近似した検定統計量 t_0, t_1の分布になります。 検出力は対立仮説における帰無仮説が棄却される領域の確率なので新たに追加された黄色の領域が 1-\betaで緑の領域が \betaになります。

効果量の決定

サンプルサイズを計算するためには有意水準 \alphaや検出力 1-\betaに加えて効果量という変数を考える必要があります。 効果量は比較している統計量にどの程度の差があるかを想定する量です。 一般的に決められた \alpha, \betaの下で大きな効果量においては相対的に小さなサンプルサイズで済みますが、小さな効果量を設定した場合は大きなサンプルサイズが必要になります。例えばそこまで大きなCVRの変化が見込まれないキャンペーンにおいてはサンプルサイズが小さい場合は仮に差があったとしても見落とす可能性があります。

効果量の定義としてはcohenが提唱しているものがあり2群の平均値の差の検定ではcohenのdと呼ばれる \frac{\mu_0 - \mu_1}{\sigma}が使われます。 サンプルサイズが非常に大きくなるとノイズを拾ったような小さな差でも有意判定されることがあるため事前に施策などによる期待される効果量を決めておくことは重要です。

サンプルサイズの計算

これまでの過程で \alpha、 1-\betaと効果量が決まったのでここからサンプルサイズを計算します。 サンプルサイズを正しく計算することでA/Bテストを走らせる期間を決定することが出来ます。 検出力を表す式からサンプルサイズを計算したいと思います。 検出力は H_1の分布での H_0が棄却される領域の確率なので以下になります

\begin{aligned} 1-\beta &= P(|t_0| \geq t_{\alpha/2}(\phi)) \\ &= P(t_0 \geq t_{\alpha/2}(\phi)) + P(t_0 \leq -t_{\alpha/2}(\phi)) \\ &\sim P(t_0 \geq t_{\alpha/2}(\phi)) \end{aligned}

ここでPは H_1の分布での確率で t_{\alpha/2}(\phi)は両側検定での有意水準でのt値です。 H_1は非心t分布になりますがサンプルサイズが大きい場合は正規近似できるので

\begin{aligned} 1-\beta &\sim P\left(\frac{\bar{x_0}-\bar{x_1}}{\sqrt{\sigma_0^2/n_0+\sigma_1^2/n_1}} \geq z_{\alpha/2}\right) \\ &\sim P\left(\frac{(\bar{x_0}-\bar{x_1})-(\mu_0-\mu_1)}{\sqrt{\sigma_0^2/n_0+\sigma_1^2/n_1}} + \frac{\mu_0-\mu_1}{\sqrt{\sigma_0^2/n_0+\sigma_1^2/n_1}} \geq z_{\alpha/2}\right) \\ &\sim p(u + \sqrt{n/2}\Delta\geq z_{\alpha/2}), \left(n_0 \sim n_1 \sim n, \Delta=\frac{\mu_0-\mu_1}{\sqrt{(\sigma_0^2+\sigma_1^2)/2}}, u \sim N(0, 1)\right) \\ z_{1-\beta} &\sim z_{\alpha/2} - \sqrt{n/2}\Delta \\ n &\sim 2\left(\frac{z_{\alpha/2} - z_{1-\beta}}{\Delta}\right)^2 \end{aligned}

サンプルサイズが少ない場合は非心t分布による補正が入り

\begin{aligned} n &\sim 2\left(\frac{z_{\alpha/2} - z_{1-\beta}}{\Delta}\right)^2 + \frac{z_{\alpha/2}^2}{4} \end{aligned}

となります。この補正は \alpha=0.05で1程度です。 これでサンプルサイズを有意水準 \alpha、検出力1-\betaと効果量 \Deltaにより計算できるようになりました。 実際に計算されたサンプルサイズまでデータを溜めて検定を行うことが出来ます。 Gunosyではredashで効果量、データの割り当てなどを指定することでサンプルサイズやデータ収集に必要な日数を計算できるようにしてあります。

ノンパラメトリック検定

データに正規分布の仮定などが出来ない場合は、分布を前提としないノンパラメトリック検定が有用です。ここでは2群のt検定に対応するWilcoxonの順位和検定を考えます。Mann-WhitneyのU検定もありますが、使用する統計量が少し異なるだけで同じ内容の検定です。これらの検定は正規性の有無に関わらず高い検出力をもつことが知られています。 順位和検定では大きさの順位を利用するため外れ値の影響も小さくなる利点もあります。

等分散な2群のデータ x_i (i=1,2,...m), y_j (j=1,2,...n)を想定した時に順位和検定の手順は以下のようになります。

  1. 2群を混ぜた N=m+n個のデータを昇順に並べて順位R_k (k=1,2,...N)を付与する。(同じ値があった場合は平均順位)

  2. 片方の群で付与された順位の和 R_x=\sum_{i=1}^{m}R_iをとる(総合計はN(N+1)/2)。

  3. 2群を混ぜたデータで帰無仮説の順位の確率分布を求める。

  4. サンプルが小さい場合は順位分布と R_xで有意水準による棄却領域とを比較する。

  5. サンプル数が大きい(>20程度)場合は平均 m(m+n+1)/2、分散 mn(m+n+1)/12の正規分布に近似できるためz検定を行う。

Pythonではscipy.stats.wilcoxonは対応のある順位和検定になってしまうので独立な2群の場合はMann-WhitneyのU検定(scipy.stats.mannwhitneyu)で検定を行うことが出来ます。

from scipy import stats
stats.mannwhitneyu(x_i, y_j)

順位和検定は2群が等分散でない場合検出力が落ちるため正確に検定出来ない問題があります。しかし、Brunner-Munzel検定を使用することで等分散でない場合の2群のノンパラメトリック検定が行えます。Pythonではscipy.stats.brunnermunzelが用意されています。

多重比較

ここまでパラメトリック/ノンパラメトリックの独立な2群での検定を考えてきましたが、ここでは3群以上での多重比較の場合を考えたいと思います。 具体的なサービスでの使用例としてはUIやロジック変更のA/Bテストなどで1つのcontrol群と2つ以上のtreatment群の比較を行うときなどで使用します。 代表的な多重比較の例として分散分析(ANOVA)がありますが、ANOVAでは特定の群間での比較は出来ないためA/Bテストなど1つのcontrol群と幾つかのtreatment群を比較したい場合は他の多重比較法を使う必要があります。 多重比較の場合でもN群あれば {}_N C_2回２群の検定を繰り返せば良さそうですがこれにはfamilywise error rate(FWER)という問題があります。

FWERは帰無仮説が正しい場合でも 1-(1-\alpha)^m (mは検定数)で少なくとも1度は帰無仮説が棄却される確率を表します。 検定数が1回の時は有意水準 \alphaと一致しますが検定回数が上がると大きく上昇します。例えば \alpha=0.05で20回検定を行うとFWER=0.64になり帰無仮説が正しい場合でも理論的には高い確率で棄却してしまいます。この問題を解決するためにFWERを増大させない多重比較法が開発されています。

FWERを調整して増大させない検定方法はt統計量を使用するTukey–Kramer(Tukey's HSD)法、Dunnett法 やノンパラメトリック検定ではTukey–Kramer法に対応するSteel‒Dwass法、Dunnett法に対応するSteel法などがあります。 統計量を使わずにp値を直接調整する方法ではBonferroni法やHolm法があります。 Bonferroni法は検定数がnの時に有意水準を \alpha \rightarrow \alpha/nに補正する方法でHolm法はこの有意水準の変換を少し緩くした方法です。 これらの方法でFWERの問題は解決されますが特にBonferroni法やHolm法は検定回数が増えた際に検出力が低くなってしまう問題があります。そこで、False Dscovery Rate(FDR)という値を調整する方法が開発されています。FWERの定義は下の表から P(v \geq 1)となりますがFDRは q=v/Rで定義されます。これは棄却された帰無仮説の中の真の帰無仮説の割合を表しています。 qの値は5%にすることが多いようですが実験の目的次第で調整します。

採択棄却合計
真の帰無仮説u(true negative)v(false positive: \alpha)n
偽の帰無仮説t(false negative: \beta)s(true positive: 1-\beta)N-n
合計N-RRN

FDRを調整する検定方法として開発されたのがBenjamini-Hochberg(BH)法です。 BH法の手順は以下のようになります。

  1. 帰無仮説 H_1,H_2,...H_nに対応したp値 P_1,P_2,...P_nを昇順に並べる。

  2. i=nとする

  3. P_i \leq \frac{i}{n}qを満たす場合次の手順に進む。満たさない場合i-1として繰り返します。

  4. H_1, H_2,...H_kの帰無仮説を棄却する。

FDRを制御する方法には他にもBH法に相関を考慮に入れてより保守的になるBenjamini and Yekutieli(BY法)やBH法で仮定されているp値の一様性が無くなる場合を考慮に入れたStorey法などがあります。 FDRを調整する方法は検出力が高い代わりに第1種の過誤を犯す確率は高くなるため実験の性質によってFWERとFDRのどちらを調整する方法かを適切に選択する必要があります。 多重検定のパッケージはRの方が揃っていますが、Pythonでもstatsmodelsのstats.multitest.multipletestsやstats.multicomp.MultiComparisonで幾つかの検定を行うことができます。

おわりに

ここまで基本的な検定の流れやパラメトリック、ノンパラメトリック検定や多重比較のお話をさせていただきました。正しい意思決定を行うにはそれぞれのケースにあった手法を選択することやデータ集計やサンプルサイズの計算などの一連の流れをスムーズに行える環境を用意しておくことが重要だと感じています。上記での方法にも様々な問題があり、例えばサンプルサイズが貯まるまで長期間待つ必要がある場合意思決定のスピードが遅くなってしまいます。これを解決するためにFWERを上昇させずに逐次的なp値のモニタリングを出来る方法なども開発されておりこのような手法にも挑戦しています。

参考文献