はじめに
おはようございます。BIチームの齊藤です。
サンタさんには善玉コレステロールと来年1月末の某ライブのチケットをお願いしようと思います。マジで頼む。
こちらの記事は Gunosy Advent Calendar 2021 の18日目の記事です。
昨日の記事は同じくBIチームの田辺さんの「オンラインホワイトボードを使った振り返りで数値意識が向上した話」でした。Good Article!
さて、みなさんは仕事でアンケートをとったことはありますか?
Webサービスでユーザー行動を分析する際には、各種の行動ログを用いたレトロスペクティブ分析や、A/Bテストを用いた施策の効果検証を行うのが一般的です。
一方でこれらの手法が使えない、または効果を発揮できない場面があります。
- 定性的指標のような、ログを用いた測定が困難な概念についての分析
- 実装に時間がかかる施策についての初期段階での調査
このような場合での分析手法の選択肢のうちの一つがアンケートです。
・・・アンケート、なんとなく簡単にシュッと実施できそうなイメージありませんか? 実はアンケートの設計と分析には様々な落とし穴が潜んでいます。

本記事では、一見簡単に行えそうなアンケートを正しく実施するための注意点や、アンケート分析の際によく用いられる統計手法について紹介していきます。
アンケートにおける注意点
「何のためにこの質問をするのか」を明確にする
アンケートの集計が終わった後で、「なんかこういう結果になったけど、これ見てこの後どうするんだっけ?」となることは避けたい事態です。
各設問について、この設問はユーザー満足度を測って目標値と比較するため、この設問はデザインに対する仮説とユーザーの感じ方との乖離を確認するため、といったように設問の目的および結果を受けてのネクストアクションのイメージを前もって固めておくことが望ましいです。
できる限りバイアスを排除する
アンケートに限った話ではありませんが、分析の対象者や実験グループの振り分けなどに何らかの偏りがある場合、得られた結果は正確なものとは言えません。
アンケート実施の際には、主に掲載場所と掲載期間の2点でバイアスが発生しやすいです。
- 掲載場所
例えばTwitter上でアンケートを掲載する場合、普段からある程度スマホを使っている人が多くなる、アンケートを呟いたアカウントをフォローしている特定の属性の人にしか届かない、といったようなバイアスがかかるため、このバイアスを前提としない設問でのアンケートは正確ではなくなります。
アプリ内やウェブページ内でアンケートを掲載する場合は、その掲載位置を訪れる人に何らかの偏りがないかなどを気にしながら検討すると良いでしょう。
- 掲載期間
例えばアプリ内で午前中のみアンケートを掲載した場合、通勤中にスマホを使用しているユーザー層の回答が多くなる、といったようなバイアスがかかる可能性があります。
私がアンケートを実施する時は基本的に1週間掲載することで時間と曜日によるバイアスを排除しています。
他にも、何らかの不満を持った人だけがアンケートに回答していないかといったような回答ユーザーの偏り(応答バイアス)についても注意が必要です。
質問文はわかりやすく、誤解のないように
アンケートでは、ユーザーインタビューやユーザーテストのようにユーザーが質問の意図を確認するということができないため、ユーザーに誤解なく伝わるように、慎重に質問文を表現する必要があります。
また質問文がわかりづらかったり、設問数が多い場合などは途中でアンケートの回答から離脱してしまう原因にもなるため注意が必要です。
その他にも、提示する質問や画像の順番でユーザーの回答を特定の選択肢に誘導させていないか、時間をかけてアンケートを実施する際に途中で設問が変わってしまうようなことはないかなど、アンケートでは気を付けるべき点が大量にあります。難しい!
よく使う統計手法
アンケートでデザインの好みやユーザー満足度を聞いたけど、結局ちゃんと差があるのかわからない・・・となった時、統計の出番です。これ以降はある程度の統計の知識があることが前提となるため、苦手な方はどのような場面が登場するかを見て「こういう質問なら統計で判定できるんだな」的な雰囲気を感じとってください。
母比率に関する検定
デザインAとBのどちらが好みかをユーザーに聞いて、結果からユーザー全体のうち過半数がA(またはB)を好んでいると言えるか、といった問題は母比率に関する検定として扱われます。
こちらについては既にたくさんの記事、参考書が存在しているため詳細に関してはここでは割愛します。興味がある方は「母比率の検定」という単語で調べてみてください。
適合度の検定
5種類のキャラクターA~Eのうちどれが一番好きかを聞いた際に、実際のキャラクターの人気が想定と一致しているかのような、期待される回答数(度数*1 )と実際に得られた(観測された)度数との当てはまりの良さを検定する問題は適合度検定で取り扱います。
種類のカテゴリーについて、ある
番目のカテゴリー
の観測される確率が
であるという帰無仮説
を考えます。
合計度数
が得られたとき、カテゴリー
の観測度数
と期待度数
(
)について次の統計検定量
は自由度
の
分布に近似的に従うことが知られています。
例:
キャラクターA~Eのうちどれが一番好きかについて100人にアンケートを取り、以下の表のような結果が得られたとします。

どのキャラクターも同じように好まれるという帰無仮説のもとで、期待される度数は表の下段のようになります。
上の表から計算される統計量は = (15-20)2/20 + (13-20)2/20 + (22-20)2/20 + (31-20)2/20 + (19-20)2/20 = 10となり、自由度4の
分布の上側5%点9.49と比較すると大きな値であることから帰無仮説は棄却され、キャラクターによる人気度に差があることがわかります。
独立性の検定
ある健康食品を摂取したグループと摂取していないグループとで健康診断で異常判定が出た人数に差があるかどうかを調査したい時のように、2つの属性AとBに関係性があるか(独立であるか)という問題では独立性検定を行います。
合計個のデータについて、属性
かつ
である観測数を
とした時、クロス集計表(分割表)で表すと以下のようになります。
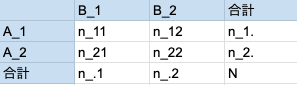
2つの属性A, Bが独立であるという帰無仮説は、: すべての
について
で表されます。
カテゴリの出現確率の推定値はそれぞれ
であるため、
の下での(
)の期待度数
は
となります。
属性Aのカテゴリ数を、属性Bのカテゴリ数を
とした時、帰無仮説
の下で次の統計検定量
は度数が大きいとき近似的に
分布に従います。このとき自由度は
となります。
例:
健康食品と健康診断の例について、以下のような分割表が得られたとします。
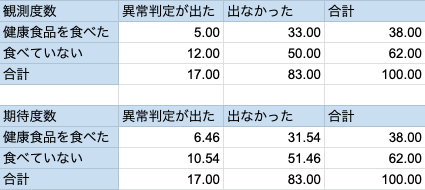
の値は
= (5-6.46)2/6.46 + (33-31.54)2/31.51 + (12-10.54)2/10.54 + (50-51.46)2/51.46 = 0.641となり、自由度1の
分布の上側5%点3.84と比較すると小さい値となり、この健康食品の摂取の有無と健康診断の結果との間には関連性があるとは言えない結果となりました。
マン・ホイットニーのU検定(ウィルコクソンの順位和検定)
グループXとYのそれぞれにユーザー満足度を10段階で聞き、グループ間の満足度に差があるか調べたい場合などには、マン・ホイットニーのU検定を利用した検定を行います。
人からなるグループ
から得られた値を
、
人からなるグループ
から得られた値を
とします。
ここで、これらをまとめたものをと表します。すなわち
となります。ここで、を小さい順に並べて1からm+nまで順位をつけたときに
の順位を
とおきます。同順位の場合は平均順位を割り付けます(例えば、同着1位が5つあった場合は(1+2+3+4+5)/5=3を割り付けます)。ここで、
とおきます。すなわち、は
の順位の和であり、
は
の順位の和です。このとき
となります。
を「
が
より大きくなる個数」とします。いま、
を小さい順に並べたものを
とし、各
に対応する順位を
とします。ここで、明らかに
は
個の
よりも大きく、同様に
は
個の
よりも大きいです。よって、
となります。同様に となり、
が導かれます。
統計検定量は
と
のうち小さい方とします。
の値が大きいとき、
と
の分布が等しいという帰無仮説のもとで
の平均と分散はそれぞれ
となることが知られているため、正規近似 を行って検定することができます。
マン・ホイットニーのU検定で検索すると、を
といった形にしている場合がありますが、
と
を用いて式変形することで同じ形のものを得ることができます。
例:
50人ずつのグループについて、サービスの満足度を10段階で質問して以下の表のような結果が得られたとします。

XとYについて順位を割り当てていきます。
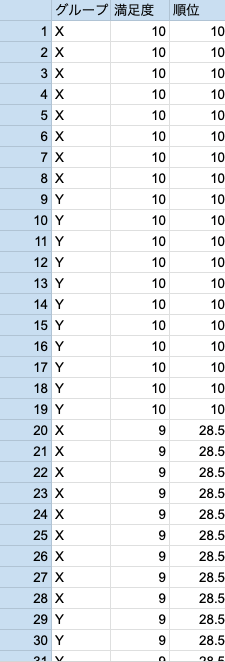
なので、
= 2628.5 - 50(50+1)/2 = 1353.5,
= 2401.5 - 50(50+1)/2 = 1126.5となり、
を統計検定量とします。
このとき、z≒-0.8513となり、グループと
で満足度に差があるとは言えない結果となります。
・・・お気づきかとは思いますが、この集計作業を手作業でするのは極めて面倒なのでPythonかなんかでやりましょう*2。面倒なことはPythonにやらせていけ
おわりに
さて、ここまでアンケート分析についての解説を行ってきました。
一見簡単そうに見えるアンケートにも、実は設計と分析はなかなかに困難であることが伝わったでしょうか?
とはいえアンケートの実施自体は簡単に行えることが多いため、まずは手を動かして経験を積んでいきましょう!
明日はiOSエンジニアの田口さんによる「iOSエンジニアがサーバサイドもやってみた話」の予定です。お楽しみに!